algodeck
Graph
A* algorithm
Complete solution to find the shortest path to a target node
Algorithm:
- Put initial state in a priority queue
- While priority queue is not empty: poll an element and inserts all neighbours
- If target is reached, update a min variable
Priority is computed using the evaluation function: f(n) = h + g where h is an heuristic (local cost to visit a node) and g is the cost so far (length of the path so far)
Backedge definition
An edge from a node to itself or to an ancestor
Best-first search algorithm
Greedy solution (non-complete) to find the shortest path to a target node
Algorithm:
- Put initial state in a priority queue
- While target not reached: poll an element and inserts all neighbours
Priority is computed using the evaluation function: f(n) = h where h is an heuristic (local cost to visit a node)
BFS & DFS graph traversal use cases
BFS: shortest path
DFS: does a path exist, does a cycle exist (memo: D for Does)
DFS stores a single path at a time, requires less memory than BFS (on average but same space complexity)
BFS and DFS graph traversal time and space complexity
Time: O(v + e) with v the number of vertices and e the number of edges
Space: O(v)
Bidirectional search
Run two simultaneous BFS, one from the source, one from the target
Once their searches collide, we found a path
If branching factor of a tree is b and the distance to the target vertex is d, then the normal BFS/DFS searching time complexity would we O(b^d)
Here it is O(b^(d/2))
Connected graph definition
If there is a path between every pair of vertices, the graph is called connected
Otherwise, the graph consists of multiple isolated subgraphs
Difference Best-first search and A* algorithms
Best-first search is a greedy solution: not complete // a solution can be not optimal
A*: complete
Dijkstra algorithm
Input: graph, initial vertex
Output: for each vertex: shortest path and previous node // The previous node is the one we are coming from in the shortest path. To find the shortest path between two nodes, we need to iterate backwards. Example: A -> C => E, D, A
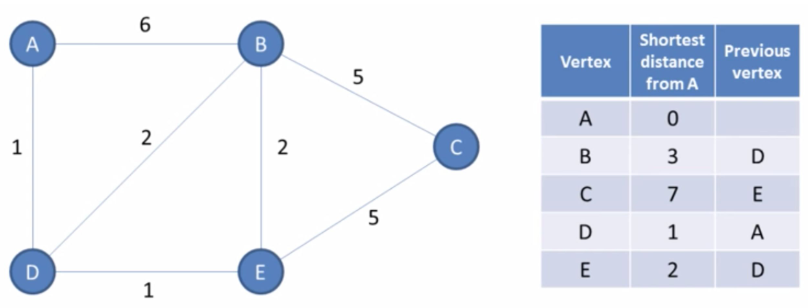
Algorithm:
- Init the shortest distance to MAX except for the initial node
- Init a priority queue where the comparator will be on the total distance so far
- Init a set to store all visited node
- Add initial vertex to the priority queue
- While queue is not empty: Poll a vertex (mark it visited) and check the total distance to each neighbour (current distance + distance so far), update shortest and previous arrays if smaller. If destination was unvisited, adds it to the queue
void dijkstra(GraphAjdacencyMatrix graph, int initial) {
Set<Integer> visited = new HashSet<>();
int n = graph.vertex;
int[] shortest = new int[n];
int[] previous = new int[n];
for (int i = 0; i < n; i++) {
if (i != initial) {
shortest[i] = Integer.MAX_VALUE;
}
}
// Entry: key=vertex, value=distance so far
PriorityQueue<Entry> minHeap = new PriorityQueue<>((e1, e2) -> e1.value - e2.value);
minHeap.add(new Entry(initial, 0));
while (!minHeap.isEmpty()) {
Entry current = minHeap.poll();
int source = current.key;
int distanceSoFar = current.value;
// Get neighbours
List<GraphAjdacencyMatrix.Edge> edges = graph.getEdge(source);
for (GraphAjdacencyMatrix.Edge edge : edges) {
// For each neighbour, check the total distance
int distance = distanceSoFar + edge.distance;
if (distance < shortest[edge.destination]) {
shortest[edge.destination] = distance;
previous[edge.destination] = source;
}
// Add the element in the queue if not visited
if (!visited.contains(edge.destination)) {
minHeap.add(new Entry(edge.destination, distance));
}
}
visited.add(source);
}
print(shortest);
print(previous);
}
Dynamic connectivity problem
Given a set of nodes and edges: are two nodes connected (directly or in-directly)?
Two methods:
- union(2, 5) // connect object 2 with object 5
- connected(1 , 6) // is object 1 connected to object 6?
Further Reading
- Dynamic Connectivity Problem by Omar El Gabry
Dynamic connectivity problem - Quick-find solution
Array of integer of size N initialized with their index (0: 0, 1: 1 etc.).
If two indexes have the same value, they belong to the same group.
- Is connected: id[p] == id[q] // O(1)
- Union: change all elements in the array whose value is equals to id[q] and set them to id[p] // O(n)
Dynamic connectivity problem - Quick-union solution
Init: integer array of size N
Interpretation: id[i] is parent of i, root parent if id[i] == i
- Is connected: check if p and q have the same parent // O(n)
- Union: set the id of p’s root to the id of q’s root // O(n)
Dynamic connectivity problem - Weighted Quick-union solution
Modify quick-union to avoid tall tree
Keep track of the size of each tree (number of nodes): extra array size[i] to count number of objects in the tree rooted at i
O(n) extra space
- Union: link root of smaller tree to root of larger tree // O(log(n))
- Is connected: root(p) == root(q) // O(log(n))
Given n tasks from 0 to n-1 and a list of relations so that a -> b means a must be scheduled before b, how to know if it is possible to schedule all the tasks (no cycle)
Solution: topological sort
If there’s a cycle in the relations, it means it is not possible to shedule all the tasks
There is a cycle if the produced sorted array size is different from n
Graph definition
A way to represent a network, or a collection of inteconnected objects
G = (V, E) with V a set of vertices (or nodes) and E a set of edges (or links)
Graph traversal: BFS
Traverse broad into the graph by visiting the sibling/neighbor before children nodes (one level of children at a time)
Iterative using a queue
Algorithm: similar with tree except we need to mark the visited nodes, can start with any nodes
Queue<Node> queue = new LinkedList<>();
Node first = graph.nodes.get(0);
queue.add(first);
first.markVisitied();
while (!queue.isEmpty()) {
Node node = queue.poll();
System.out.println(node.name);
for (Edge edge : node.connections) {
if (!edge.end.visited) {
queue.add(edge.end);
edge.end.markVisited();
}
}
}
Graph traversal: DFS
Traverse deep into the graph by visiting the children before sibling/neighbor nodes (traverse down one single path)
Walk through a path, backtrack until we found a new path
Algorithm: recursive or iterative using a stack (same algo than BFS except we use a queue instead of a stack)
How to compute the shortest path between two nodes in an unweighted graph
BFS traversal by using an array to keep track of the min distance distances[i] gives the shortest distance between the input node and the node of id i
Algorithm: no need to keep track of the visited node, it is replaced by a test on the distance array
Queue<Node> queue = new LinkedList<>();
queue.add(parent);
int[] distances = new int[graph.nodes.size()];
Arrays.fill(distances, -1);
distances[parent.id] = 0;
while (!queue.isEmpty()) {
Node node = queue.poll();
for (Edge edge : node.connections) {
if (distances[edge.end.id] == -1) {
queue.add(edge.end);
distances[edge.end.id] = distances[node.id] + 1;
}
}
}
How to detect a cycle in a directed graph
Using DFS by marking the visited nodes, there is a cycle if a visited node is also part of the current stack
The stack can be managed as a boolean array
boolean isCyclic(DirectedGraph g) {
boolean[] visited = new boolean[g.size()];
boolean[] stack = new boolean[g.size()];
for (int i = 0; i < g.size(); i++) {
if (isCyclic(g, i, visited, stack)) {
return true;
}
}
return false;
}
boolean isCyclic(DirectedGraph g, int node, boolean[] visited, boolean[] stack) {
if (stack[node]) {
return true;
}
if (visited[node]) {
return false;
}
stack[node] = true;
visited[node] = true;
List<DirectedGraph.Edge> edges = g.getEdges(node);
for (DirectedGraph.Edge edge : edges) {
int destination = edge.destination;
if (isCyclic(g, destination, visited, stack)) {
return true;
}
}
// Backtrack
stack[node] = false;
return false;
}
How to detect a cycle in an undirected graph
Using DFS
Idea: for every visited vertex v, if there is an adjacent u such that u is already visited and u is not the parent of v, then there is a cycle
public boolean isCyclic(UndirectedGraph g) {
boolean[] visited = new boolean[g.size()];
for (int i = 0; i < g.size(); i++) {
if (!visited[i]) {
if (isCyclic(g, i, visited, -1)) {
return true;
}
}
}
return false;
}
private boolean isCyclic(UndirectedGraph g, int v, boolean[] visited, int parent) {
visited[v] = true;
List<UndirectedGraph.Edge> edges = g.getEdges(v);
for (UndirectedGraph.Edge edge : edges) {
if (!visited[edge.destination]) {
if (isCyclic(g, edge.destination, visited, v)) {
return true;
}
} else if (edge.destination != parent) {
return true;
}
}
return false;
}
How to name a graph with directed edges and without cycle
Directed Acyclic Graph (DAG)
How to name a graph with few edges and with many edges
Sparse: few edges
Dense: many edges
How to name the number of edges
Degree of a vertex
How to represent the edges of a graph (structure and complexity)
- Using an adjacency matrix: two-dimensional array of boolean with a[i][j] is true if there is an edge between node i and j
- Time complexity: O(1)
- Space complexity: O(v²) with v the number of vertices
Problem:
- If graph is undirected: half of the space is useless
- If graph is sparse, we still have to consume O(v²) space
- Using an adjacency list: array (or map) of linked list with a[i] represents the edges for the node i
- Time complexity: O(d) with d the degree of a vertex
- Space complexity: O(2*e) with e the number of edges
Topological sort complexity
Time and space: O(v + e)
Topological sort technique
If there is an edge from U to V, then U <= V
Possible only if the graph is a DAG
Algo:
- Create a graph representation (adjacency list) and an in degree counter (Map<Integer, Integer>)
- Zero them for each vertex
- Fill the adjacency list and the in degree counter for each edge
- Add in a queue each vertex whose in degree count is 0 (source vertex with no parent)
- While the queue is not empty, poll a vertex from it then decrement the in degree of its children (no removal)
To check if there is a cycle, we must compare the size of the produced array to the number of vertices
List<Integer> sort(int vertices, int[][] edges) {
if (vertices == 0) {
return Collections.EMPTY_LIST;
}
List<Integer> sorted = new ArrayList<>(vertices);
// Adjacency list graph
Map<Integer, List<Integer>> graph = new HashMap<>();
// Count of incoming edges for each vertex
Map<Integer, Integer> inDegree = new HashMap<>();
for (int i = 0; i < vertices; i++) {
inDegree.put(i, 0);
graph.put(i, new LinkedList<>());
}
// Init graph and inDegree
for (int[] edge : edges) {
int parent = edge[0];
int child = edge[1];
graph.get(parent).add(child);
inDegree.put(child, inDegree.get(child) + 1);
}
// Create a source queue and add each source (a vertex whose inDegree count is 0)
Queue<Integer> sources = new LinkedList<>();
for (Map.Entry<Integer, Integer> entry : inDegree.entrySet()) {
if (entry.getValue() == 0) {
sources.add(entry.getKey());
}
}
while (!sources.isEmpty()) {
int vertex = sources.poll();
sorted.add(vertex);
// For each vertex, we will decrease the inDegree count of its children
List<Integer> children = graph.get(vertex);
for (int child : children) {
inDegree.put(child, inDegree.get(child) - 1);
if (inDegree.get(child) == 0) {
sources.add(child);
}
}
}
// Topological sort is not possible as the graph has a cycle
if (sorted.size() != vertices) {
return new ArrayList<>();
}
return sorted;
}
Travelling salesman problem
Find the shortest possible route that visits every city (vertex) exactly once
Possible solutions:
- Greedy: nearest neighbour
- Dynamic programming: compute optimal solution for a path of length n by using information already known for partial tours of length n-1 (time complexity: n^2 * 2^n)
Two types of graphs
Directed graph (with directed edges)
Undirected graph (with undirected edges)