algodeck

Tree

2-3 tree

Self-balanced BST => O(log n) complexity

Either:

• 2-node: contains a single value and has two children
• 3-node: contains two values and has three children
• Leaf: 1 or 2 keys

Insert: find proper leaf and insert the value in-place. If the leaf has 3 values (called temporary 4-node), split the node into three 2-node and insert the middle value into the parent.

#tree

AVL tree

If tree is not balanced, rearange the nodes with single or double rotations

#tree

B-tree complexity: access, insert, delete

All: O(log n)

#complexity #tree

B-tree: definition and use case

Self-balanced BST => O(log n) complexity

Can have more than two children (generalization of 2-3 tree)

Use-case: huge amount of data that cannot fit in main memory but disk space.

Height is kept low to reduce the disk accesses.

Match how page disk are working

#tree

Balanced binary tree definition

The balance factor of each node (the difference between the two subtree heights) should never exceed 1

Guarantee of O(log n) search

#tree

Balanced BST use case: B-tree, Red-black tree, AVL tree

• B-tree: paging from disk (database)
• Red-black tree: fairly frequents inserts, deletes or retrievals
• AVL tree: many retrievals, infrequent inserts and deletes

#tree

BFS and DFS tree traversal time and space complexity

BFS: time O(v), space O(v)

DFS: time O(v), space O(h) (height of the tree)

#complexity #tree

Binary tree BFS traversal

Level order traversal (level by level)

Iterative algorithm: use a queue, put the root, iterate while queue is not empty

Queue<Node> queue = new LinkedList<>();
queue.add(root);

while(!queue.isEmpty()) {
	Node node = queue.poll();
	visit(node);

	if(node.left != null) {
		queue.add(node.left);
	}
	if(node.right != null) {
		queue.add(node.right);
	}
}

#tree

Binary tree definition

Tree with each node having up to two children

#tree

Binary tree DFS traversal: in-order, pre-order and post-order

• In-order: left-root-right
• Pre-order: root-left-right
• Post-order: left-right-root

It’s depth first so:

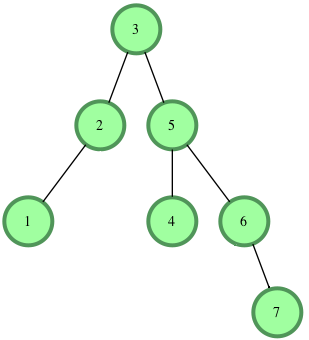
• In-order: 1, 2, 3, 4, 5, 6, 7
• Pre-order: 3, 2, 1, 5, 4, 6, 7
• Post-order: 1, 2, 4, 7, 6, 5, 3

#tree

Binary tree: complete

Every level of the tree is fully filled, with last level filled from the left to the right

#tree

Binary tree: full

Each node has 0 or 2 children

#tree

Binary tree: perfect

2^l - 1 nodes with l the level: 1, 3, 7, etc. nodes

Every level is fully filled

#tree

BST complexity: access, insert, delete

If not balanced O(n)

If balanced O(log n)

#complexity #tree

BST definition

Binary tree in which every node must fit the property: all left descendents <= n < all right descendents

Implementation: optional key, value, left, right

#tree

BST delete algo and complexity

Find inorder successor and swap it

Average: O(log n)

Worst: O(h) if not self-balanced BST, otherwise O(log n)

#complexity #tree

BST insert algo

Search for key or value (by recursively going left or right depending on the comparison) then insert a new node or reset the value (no swap)

Complexity: worst O(n)

public TreeNode insert(TreeNode root, int a) {
	if (root == null) {
		return new TreeNode(a);
	}

	if (root.val <= a) { // Left
		root.left = insert(root.left, a);
	} else { // Right
		root.right = insert(root.right, a);
	}

	return root;
}

#tree

BST questions prerequisite

Is it a self-balanced BST? (impacts: O(log n) time complexity guarantee)

#tree

Complexity to create a trie

Time and space: O(n * l) with n the number of words and l the longest word length

#complexity

Complexity to insert a key in a trie

Time: O(k) with k the size of the key

Space: O(1) iterative, O(k) recursive

#complexity #tree

Complexity to search for a key in a trie

Time: O(k) with k the size of the key

Space: O(1) iterative or O(k) recursive

#complexity #tree

Given a binary tree, algorithm to populate an array to represent its level-by-level traversal

Solution: BFS by popping only a fixed number of elements (queue.size)

public static List<List<Integer>> traverse(TreeNode root) {
	List<List<Integer>> result = new LinkedList<>();
	Queue<TreeNode> queue = new LinkedList<>();
	queue.add(root);
	while (!queue.isEmpty()) {
		List<Integer> level = new ArrayList<>();
		
		int levelSize = queue.size();
		// Pop only levelSize elements
		for (int i = 0; i < levelSize; i++) {
			TreeNode current = queue.poll();
			level.add(current.val);
			if (current.left != null) {
				queue.add(current.left);
			}
			if (current.right != null) {
				queue.add(current.right);
			}
		}
		result.add(level);
	}
	return result;
}

#tree

How to calculate the path number of a node while traversing using DFS?

Example: 1 -> 7 -> 3 gives 173

Solution: sum = sum * 10 + n

private int dfs(TreeNode node, int sum) {
	if (node == null) {
		return 0;
	}

	sum = 10 * sum + node.val;

	// Do something
}

#tree

Min (or max) value in a BST

Move recursively on the left (on the right)

#tree

Red-Black tree

Self-balanced BST => O(log n) complexity

• Root node always black
• Incoming node is red
• Red violation: child and parent are red
• Resolve violation by recoloring and/or restructuring

Further Reading

Binary Trees: Red Black by David Pynes

#tree

Red-black tree complexity: access, insert, delete

All: O(log n)

#complexity #tree

Reverse a binary tree algo

public void reverse(Node node) {
	if (node == null) {
		return;
	}

	Node temp = node.right;
	node.right = node.left;
	node.left = temp;

	reverse(node.left);
	reverse(node.right);
}

#tree

Trie definition, implementation and use case

Tree-like data structure with empty root and where each node store characters

Each path down the tree represent a word (until a null node that represents the end of the word)

Usually implemented using a map of children (or a fixed size array with ASCII charset for example)

Use case: dictionnary (save memory)

Also known as prefix tree

#tree

Why to use BST over hash table

Sorted keys

#tree

This site is open source. Improve this page.